Ma trận là đối tượng cơ bản của Đại số cao cấp, ma trận có rất nhiều ứng dụng trong Toán học cũng như trong các ngành khoa học khác.
Bạn đang xem: Công thức tính định thức cấp 3
Bàn về ma trận thì có rất nhiều chủ đề, nhiều phép tính. Ví dụ như phép tính cộng, phép tính nhân, tính định thức, tìm ma trận nghịch đảo, tìm hạng, …
Và trong bài viết ngày hôm nay mình sẽ hướng dẫn cho các bạn cách tính định thức của ma trận cấp ba.
Tại sao lại là tính định thức? Tại sao lại là ma trận cấp ba?
Vâng, tại vì thao tác tính định thức là thao tác thường gặp nhất khi làm việc với ma trận, còn ma trận cấp ba (ma trận vuông cấp 3 x 3) cũng là ma trận vuông thường gặp nhất trong các ma trận vuông
I. Ma trận là gì?
Trong toán học thì Ma trận là bảng sắp xếp số liệu (gọi là phần từ của ma trận) thành hàng và cột.
Ma trận có thể có một hoặc nhiều chiều, được biểu thị bằng số hàng và số cột.
Khi định nghĩa một ma trận ta cần chỉ rõ số hàng và số cột cùng trường số của các phần tử có nó.
Ma trận $\left(\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right)$ còn được kí hiệu là $\left<\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right>$
Định thức của ma trận được ký hiệu là $\left|\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right|$
Ma trận trong tiếng Anh là Matrix, định thức là Determinant và thường được viết tắt là det
Phương pháp #1: Phương pháp Toán học
Dưới đây là ba cách tính định thức của ma trận vuông cấp 3 x 3 thường được sử dụng nhất.
Cách 1. Quy tắc tam giácQuy tắc Tam giác về bản chất tương tự như Quy tắc của Sarrus.

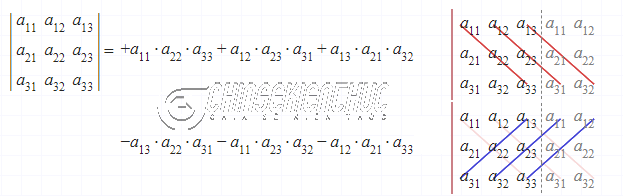
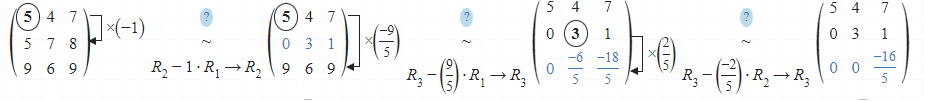





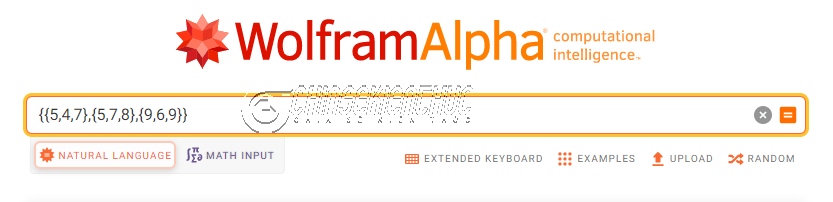

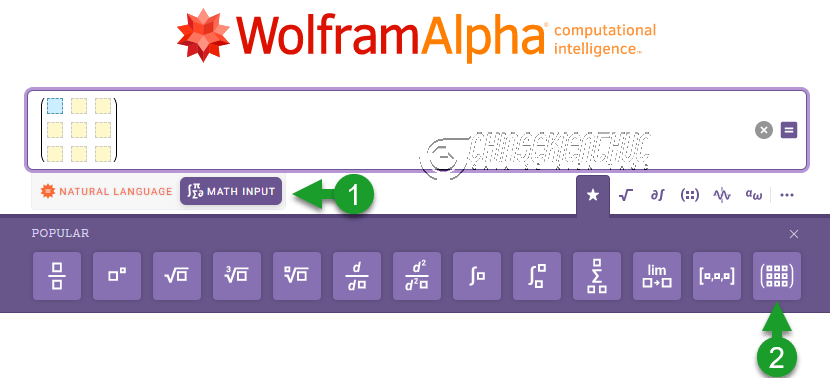
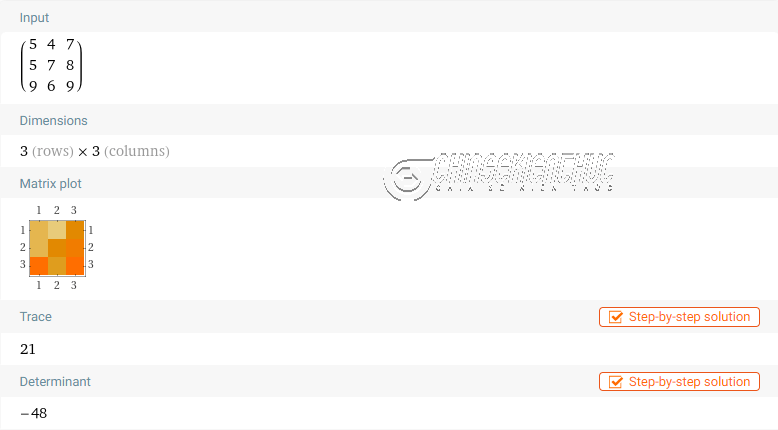
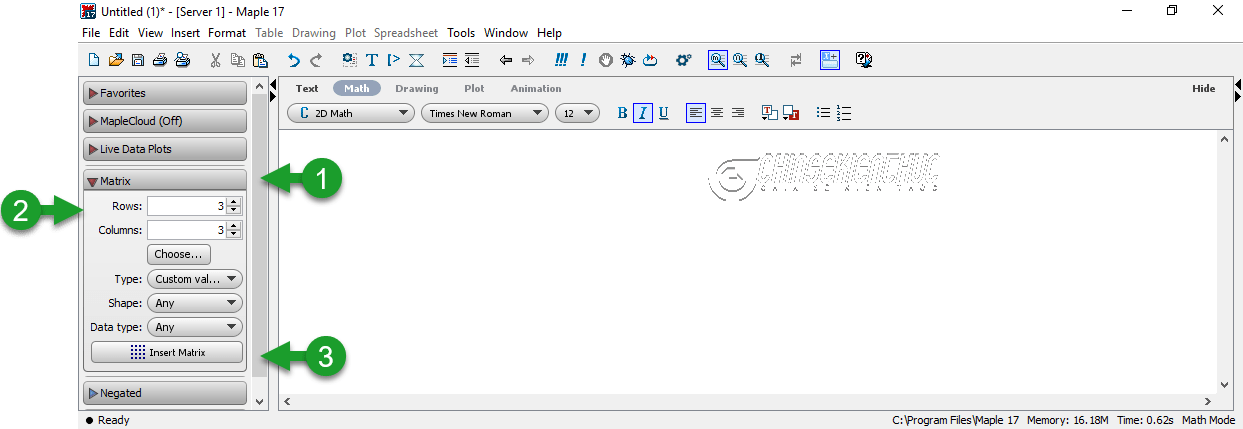
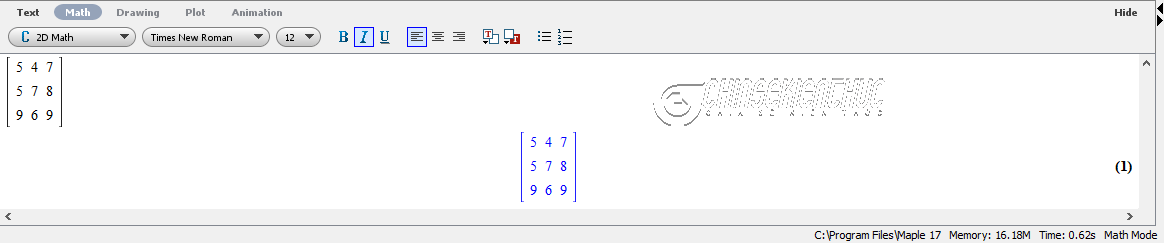
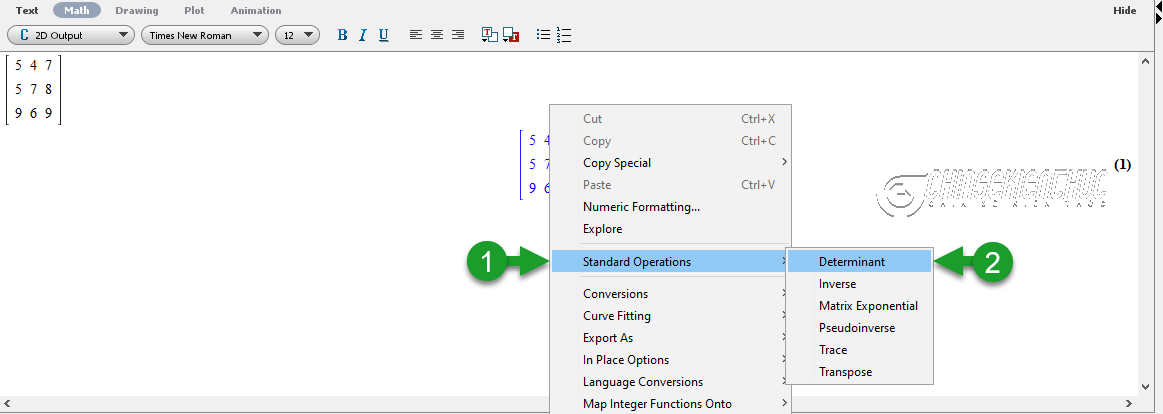
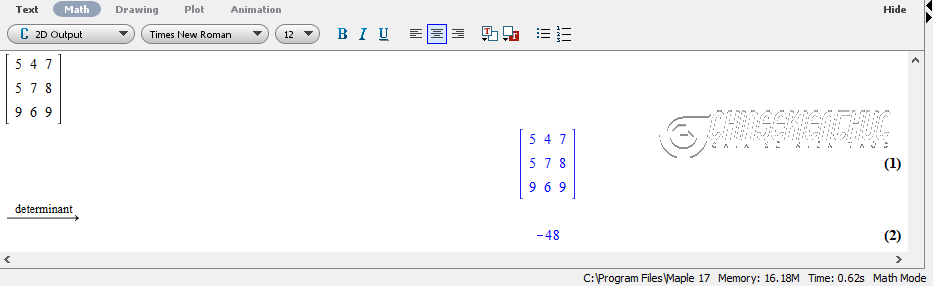
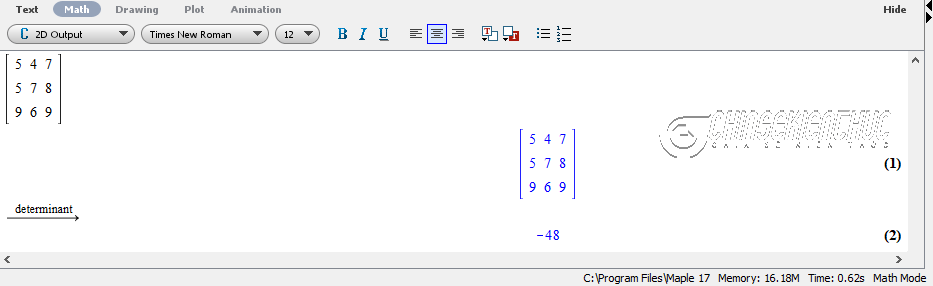
Nhận xét: Phần mềm Maple có thể tính được định thức của ma trận vuông cấp bất kì và rất nhiều ứng dụng khác nữa.
II. Lời kết
Vâng, như vậy là mình đã hướng dẫn xong cho các bạn 4 cách tính định thức của ma trận cấp ba rồi ha.
Khi được yêu cầu tính định thức của ma trận vuông cấp 3×3 …
Nếu cho dưới dạng tự luận thì bạn có thể áp dụng Cách 2, Cách 3, Cách 4 của Phương pháp 1Nếu cho dưới dạng trắc nghiệm thì áp dụng phương pháp máy tính CASIO fx-580VN X.Các bạn hãy linh hoạt áp dụng nhé. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Bài viết dưới đây tmec.edu.vn sẽ giúp các bạn hiểu rõ hơn về định thức ma trận qua các dạng bài tập tính định thức cấp 4, tính định thức ma trận cấp 5 trong chương trình toán cao cấp môn đại số và hình học giải tích.
Xem thêm:
1. Định thức ma trận là gì?
Định thức ma trận là giá trị vô hướng được tính cho một ma trận vuông nhất định. Với định thức trong đại số tuyến tính, định thức thường được tính bằng cách sử dụng các phần tử của ma trận vuông. Tính định thức được sử dụng để giải quyết giải hệ phương trình tuyến tính, tính ma trận nghịch đảo của ma trận,…Định thức của ma trận được biểu diễn bằng hai dòng dọc hoặc đơn giản bằng cách viết det và viết tên ma trận. ví dụ. | A |, det (A), det AĐịnh thức ma trận cấp 2: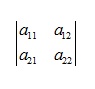
|A| =a11.a22 – a21.a12
Về mặt hình học, định thức được xem như là hệ số tỷ lệ thể tích của phép biến đổi tuyến tính được xác định bởi ma trận. Nó cũng được biểu thị bằng thể tích của n chiều song song được gạch chéo bởi vectơ cột hoặc hàng của ma trận. Định thức là dương hoặc âm khi ánh xạ tuyến tính bảo toàn hoặc thay đổi hướng của không gian n.
Ví dụ 1: Tính định thức ma trận cấp 2 sau:
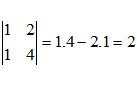

|A| =(a11.a22.a33 + a21.a32.a13 + a12.a23.a31 ) – (a13.a22.a31 + a11.a23.a32 + a12.a21.a33 )
Ví dụ 2: Giải định thức ma trận bằng phương pháp tam giác
2. Các định thức đặc biệt

3. Các tính chất của định thức ma trận
1.det (A.B) = det(A).det(B)
2.det ( AT ) = det (A)
3.Nếu đổi chỗ 2 hàng ( 2 cột ) thì det đổi dấu
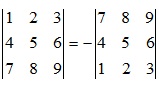
4.Nếu det
A có 1 cột hoặc 1 hàng = 0 thì định thức A =0
5.Nếu det có 2 hàng ( 2 cột ) tỉ lệ thì det A=0
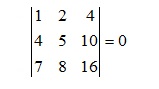
6.Nếu nhân 1 hàng, 1 cột với một số k ≠ 0 thì det mới gấp k lần det cũ
7.Nếu A là ma trận vuông cấp n thì det (k
A) = kn .det (A)
Ví dụ: A3×3 , det(A) = 5 ⇒ det(2A) = 23.5= 40
8.Tách định thức
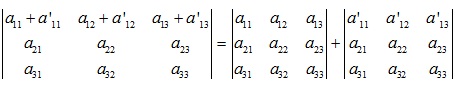
9.Rút nhân tử chung của 1 hàng, 1 cột ra ngoài định thức
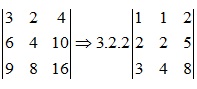
4. Tính định thức bằng phép biến đổi siêu cấp chuyển về dạng tam giác trên
Ví dụ 3: Tính định thức ma trận
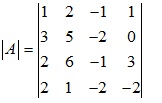
Giải:
Các bước thực hiện:
Nhân hàng 1 với -3 vào hàng 2 để xuất hiện phần tử 0a21=(-3).1 + 3 =0a22=(-3).2+5=-1a23=(-3).(-1)+(-2)=1a24=(-3).1+0=-3Tương tự nhân hàng 1 với -2 vào hàng 3, nhân hàng 1 với -2 vào hàng 1 ta được
Bài tập tính định thức ma trận
Bài 1: Tính định thức cấp 2 sau:
Bài 2: Biết các số 204,527,255 chia hết cho 17. Chứng minh định thức d chia hết cho 17
Giải
Nhân cột thứ nhất với 100 rồi cộng vào cột cuối
Nhân cột thứ hai với 10 rồi cộng vào cột cuối
Kết luận định thức chia hết cho 17 vì tích có thừa số 17
Bài 3: Cho a là ma trận vuông cấp 3 có det(a) = 3. định thức của ma trận 2a là
Hướng dẫn giải
Áp dụng công thức: det (k
A) = kn .det (A)
Ta có: det(a) = 3 ⇒ det(2a) = 23.3= 24
Bài 4: Tính định thức ma trận cấp 4

Ví dụ tính định thức cấp 4:
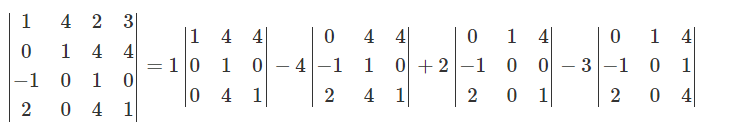
Bài 5: Tính định thức ma trận cấp 5

Tải file tài liệu lý thuyết và bài tập vận dụng định thức ma trận PDF
Nhập mã xác thực để lấy link: